
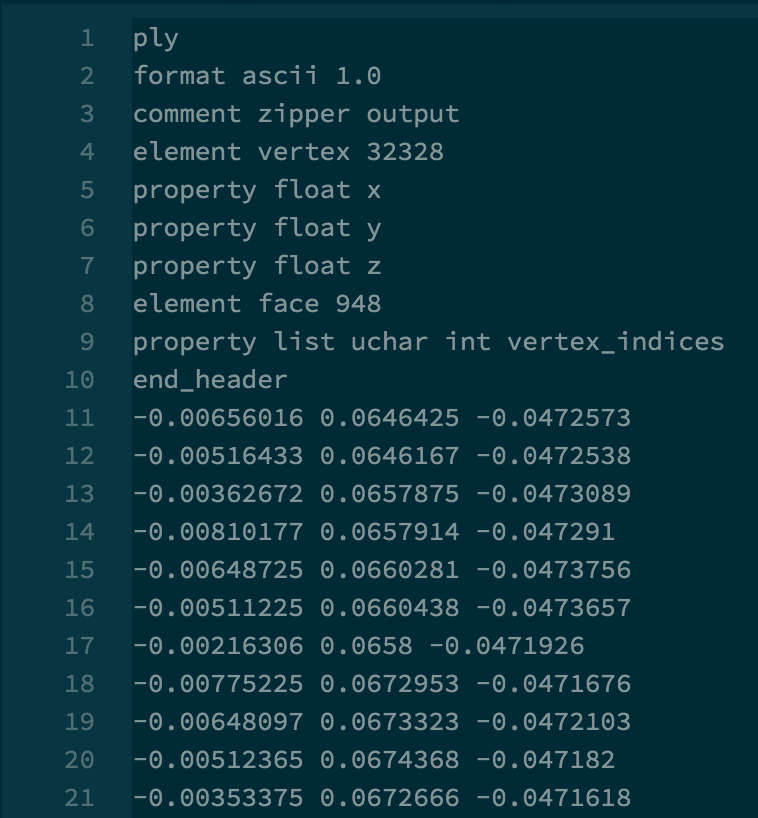
void MeshEdit::renderPoints(PointCloud& point_cloud) {
std::vector vertices = point_cloud.vertices;
DrawStyle *style = &defaultStyle;
setColor(style->vertexColor);
glPointSize(style->vertexRadius);
for (Vector3D v : vertices) {
glBegin(GL_POINTS);
glVertex3d(v.x, v.y, v.z);
glEnd();
}
}
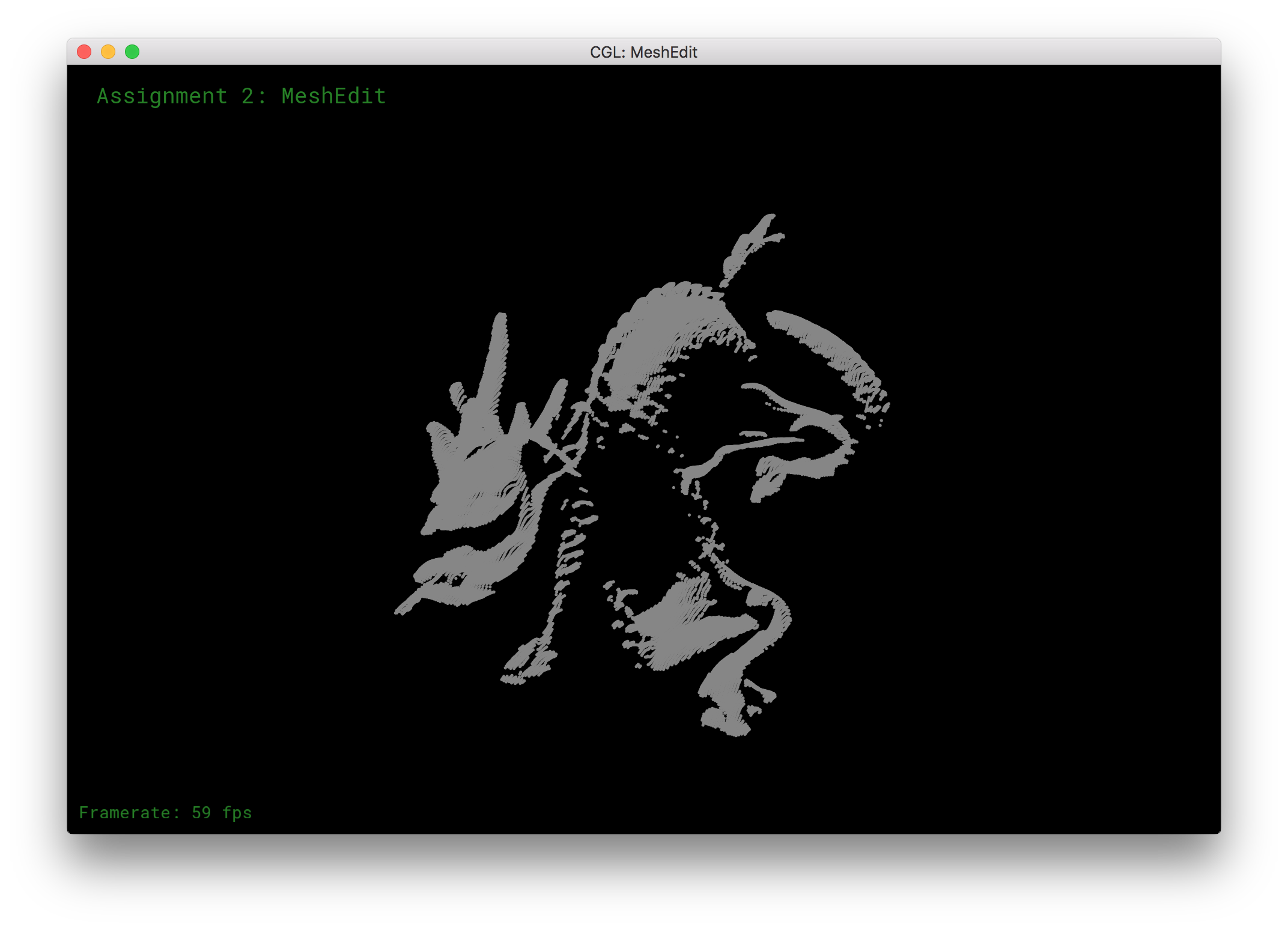
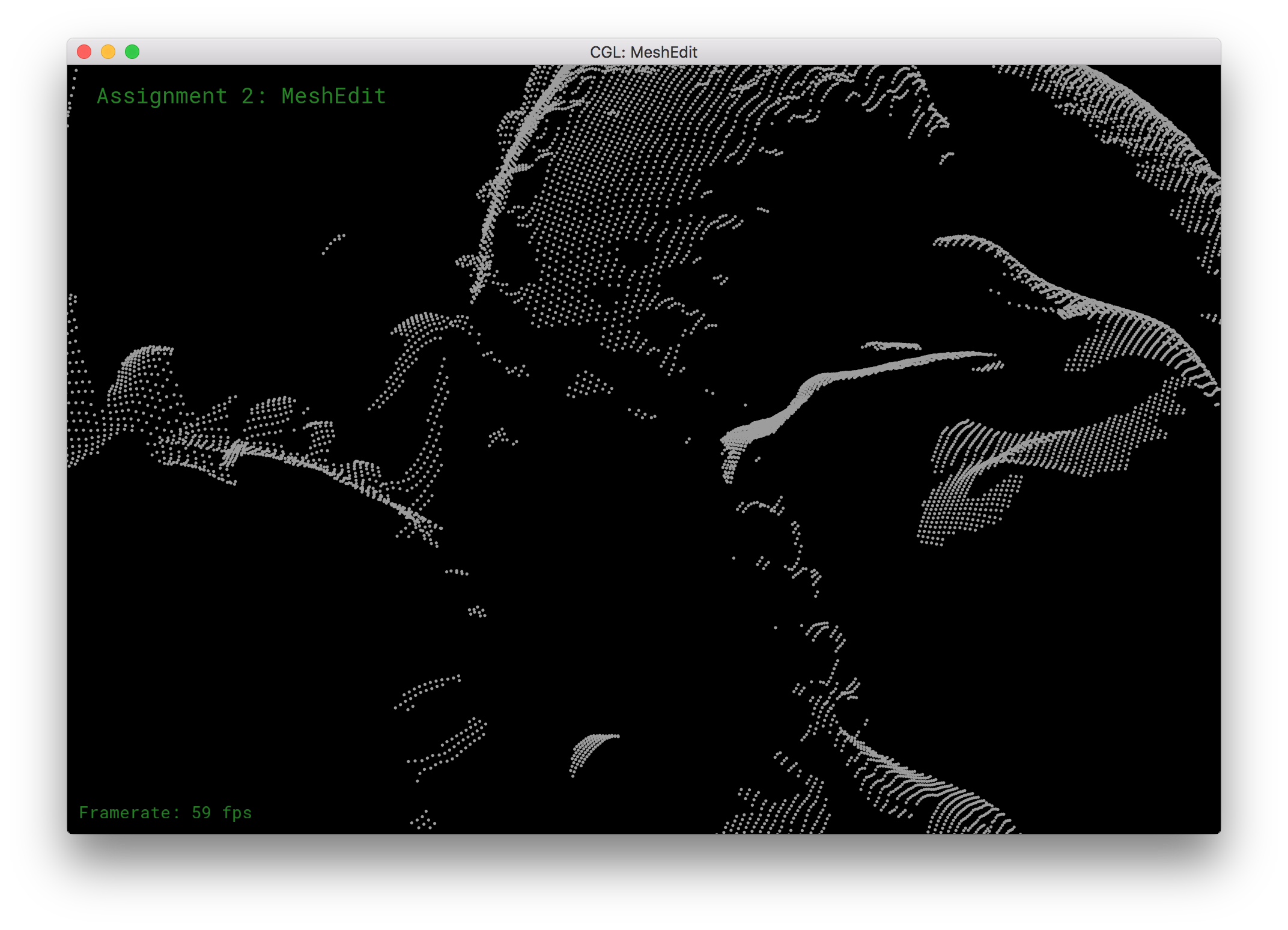
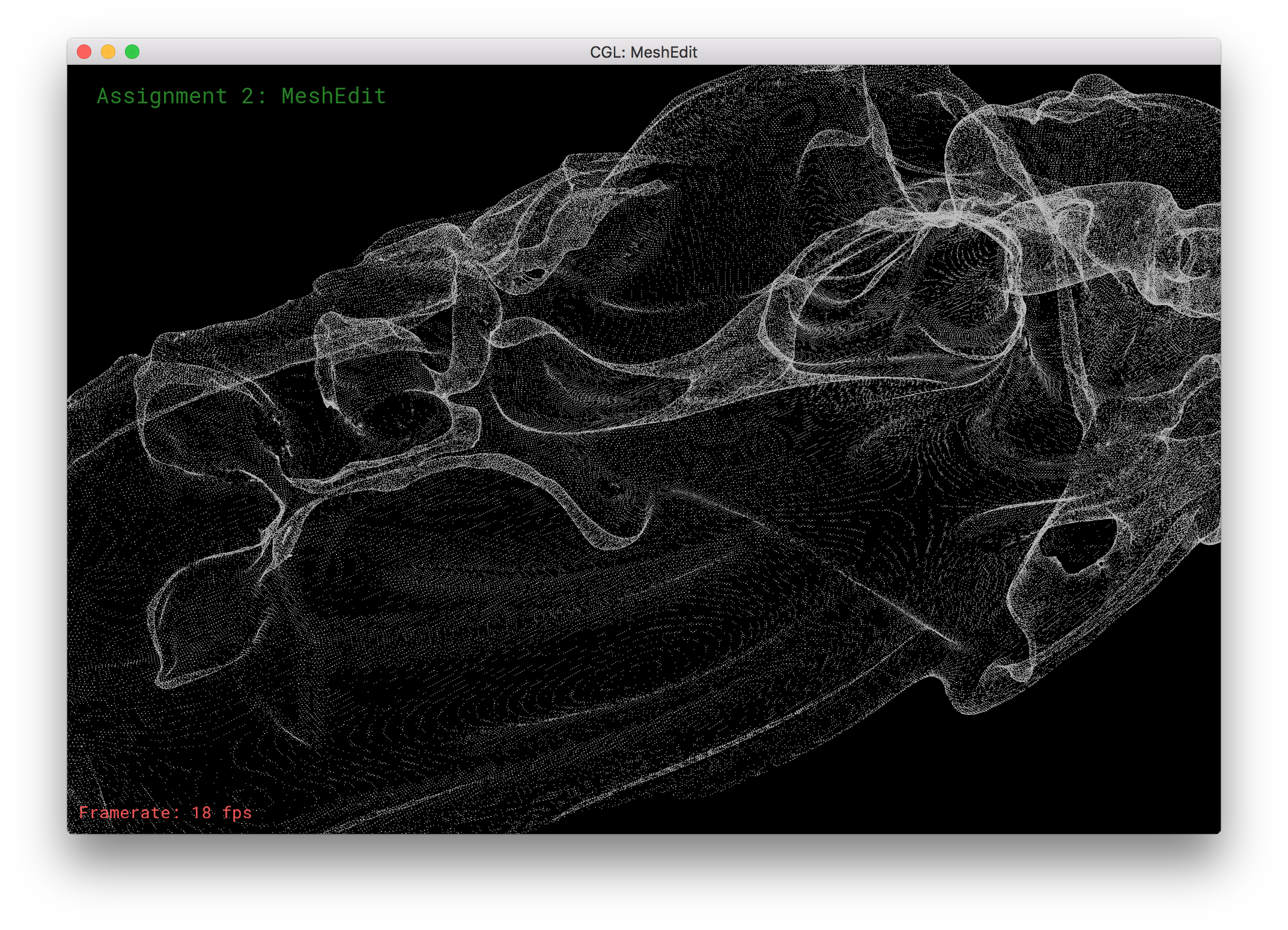
Data Structures: In order to implement the Ball Pivoting algorithm, we first had to set up a couple data structures, namely BPAEdge, BPALoop, and BPAFront.
BPAFront encapsulates the growing mesh and keeps track of all point and polygons at all times. The name Front, refers to the set of active edges (contained in Loops) that we are currently considering in order to expand the mesh. There is a single Front per mesh.
BPALoop is simply a linked list wrapper of edge that stores a pointer to the first edge in the list. The front contains a list of Loops that are currently being expanded. Loops may merge into each other or break apart as a result of join/glue operations.
BPAEdge was necessary because the ball pivot algorithm pivots over an edge. Half edges added unnecessary complexity, while the polygon soup and vertices lacked the relationship between points i and j that we needed. We only keep track of edges on the constantly expanding loop front, so every edge must have a corresponding triangle. We keep track of the third point and call it o; we will need it for our calculations later on.
Algorithm: The Ball Pivot algorithm consists of 2 main parts, the Ball Pivot step in which we discover new points and add to the mesh we are currently building on, and Seed Triangle selection, which occurs when ball pivoting gets stuck and requires us to select a new set of edges to expand on. This continues until we've considered all points that the ball can reach.
while true
1. Ball Pivot
e_ij = get_active_edge(F)
while (e_ij):
k = ball_pivot(e_ij)
if (k && (not_used(k) || on_front(k)))
output_triangle(i, k, j)
join(e_ij, k , F)
if (e_ki in F) glue(e_ik, e_ki , F)
if (e_jk in F) glue(e_kj, e_jk, F)
else
mark_as_boundary(e_ij)
e_ij = get_active_edge(F)
2. Find Seed Triangle
(i, j, k) = find_seed_triangle()
if ((i, j, k))
output_triangle(i, j, k)
insert_edge(e_ij, F)
insert_edge(e_jk, F)
insert_edge(e_ki, F)
else
return
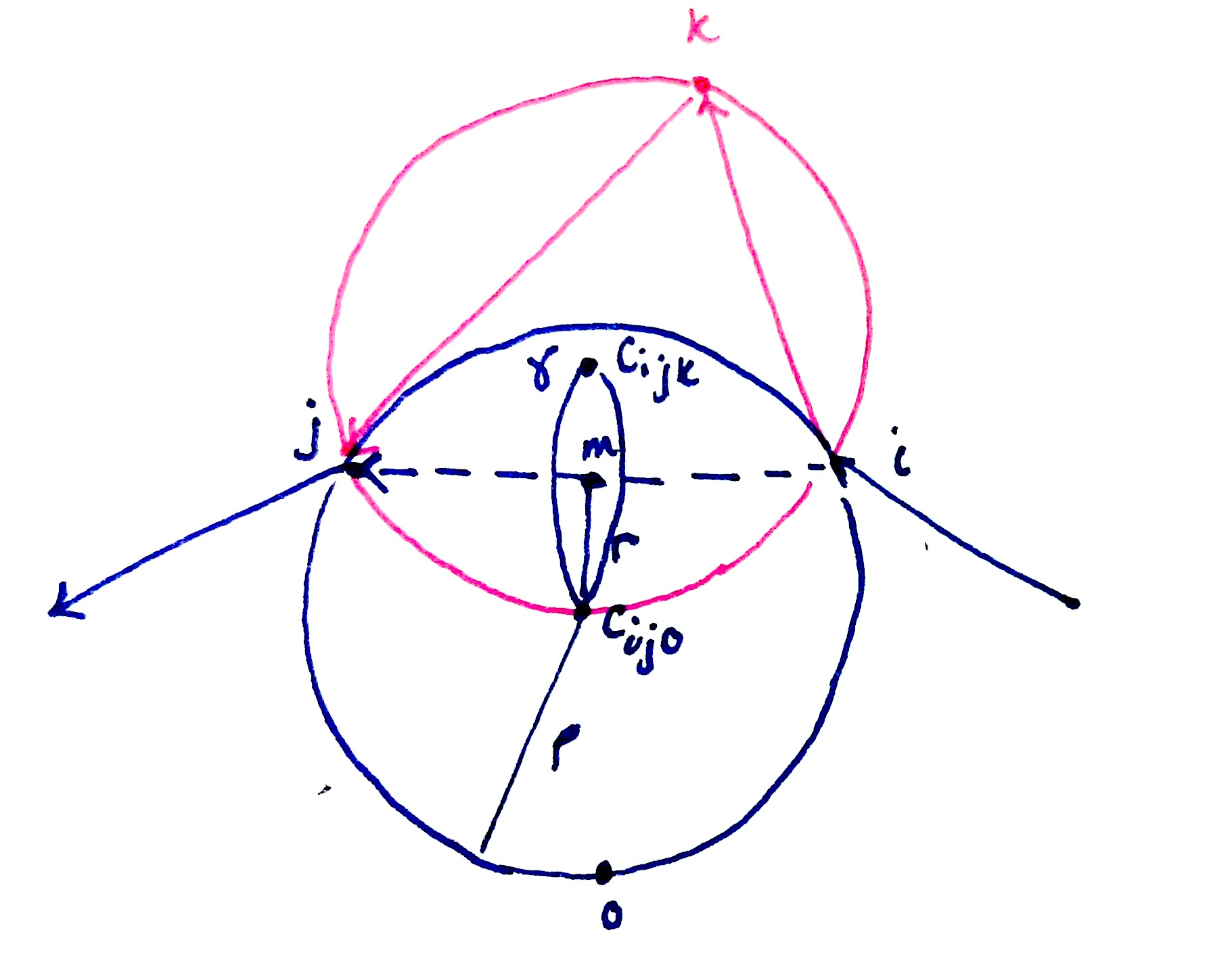
1. Ball Pivot First we select an active edge from the front. An active edge is any edge that has not been fully explored yet and thus has the opportunity for expansion. We then find all points in a 2*rho radius from the midpoint m between i and j. These are our candidate points. For each candidate point x, we calculate the center of the sphere of radius rho that touches i, j and x: c_ijx. r is the distance from m to the center of the current center of the ball, c_ijo. For each calculated center c_ijx we check if it is on the circle gamma, defined by the radius r and center m, perpendicular to the pivot edge ij. We then choose the c_ijx that we encounter first while pivoting on the edge.
Then we have found k = x, we need to incorporate the triangle ijk into our mesh and update our loop and other pointers. We expand the loop to incorporate edges ik and kj, and we remove edge ij. This operation is described as a join operation on an edge and point in the pseudocode above.
As our loop expands to fit whatever complex geometry the point cloud describes, we may find ourselves having to break apart loops creating more loops, or merging loops into a single loop. These operations are called glue operations. The glue operations ensure that at the end of the while loop, all our loops merge and we are left with a single mesh. We chose not too include glue operations as they were very complicated to implement, and while we were left with multiple meshes, they still described all the points in the point cloud reachable with our rho-sphere.
2. Find Seed Triangle Seed triangle selection is very similar to finding the next position of the sphere in the ball pivot step. We find all pairs of points in a radius 2*rho of a random, unused point. Then we verify that sphere of radius rho can lie on these three points. Finally, we check that the sphere does not contain any other data points and that it lies on the "outside" of the point cloud. However, since we didn't have vertex normals to work with, we were unable to tell where the ball was.
Sphere Center from 3 points and a radius
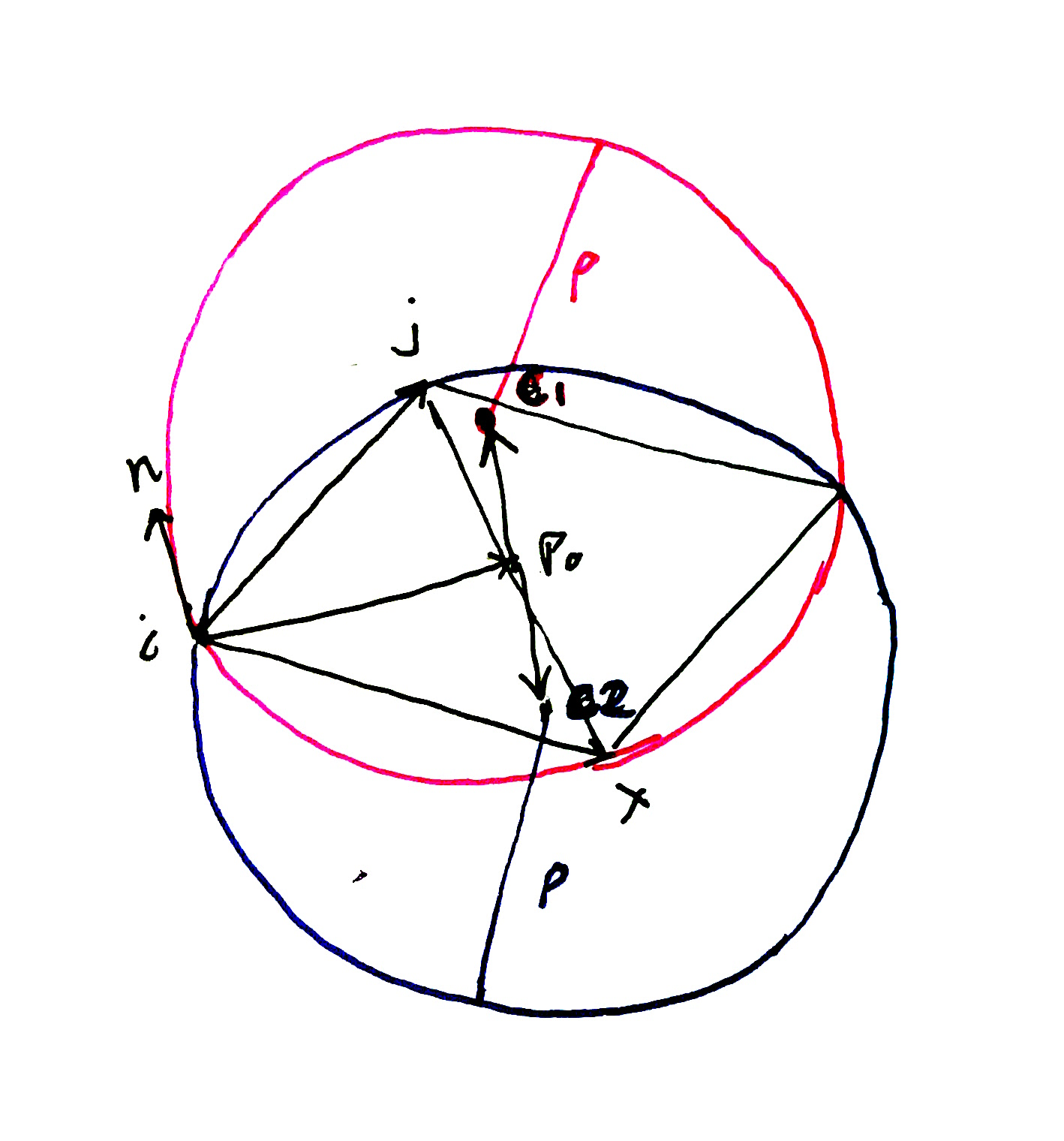
One of the most common problems in this algorithm is finding a the center of a sphere with radius rho from 3 points. Given any three points i, j and x, we can form a parallelogram. The center of the parallelogram (p0) lies on the same line as the 0, 1 or 2 sphere centers that exist for our points. To find the distance t1, t2 we need to travel on the line p, we use the Pythagorean theorem.
ji = j-i
xi = x-i
n = cross(ji, xi)
p0 = cross(dot(ji, ji) * xi - dot(xi, xi) * ji, n) / (2 * dot(n, n)) + i
t1 = sqrt((rho*rho - dot(p0-i, p0-i))/ dot(n, n))
t2 = -sqrt((rho^2 - dot(p0-i, p0-i))/ dot(n, n))
c1 = p0 + (n * t1)
c2 = p0 + (n * t2)

Collapse Edges:
Most of the popular algorithms for simplifying meshes include iterative edge contraction. Therefore, to use these algorithms we have to implement the ability to collapse edges. To do so we have to remove the selected edge from the mesh, along with the faces, halfedges and vertex that will no longer be needed. While doing this we have to make sure that all of the remaining mesh features are correctly re-attached to each other. Here is a diagram of an edge collapse:
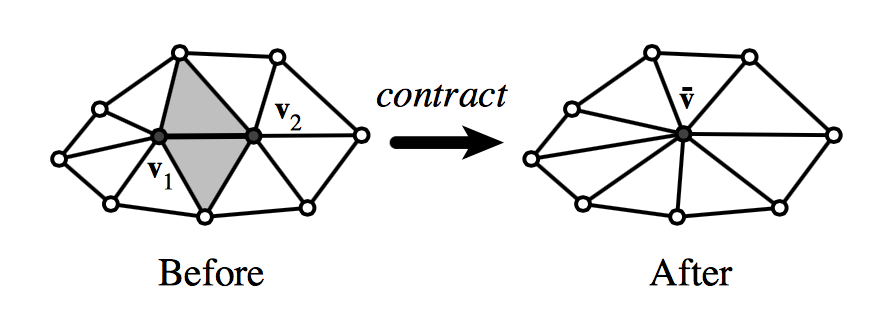
HalfedgeIter h = v->halfedge(); // get one of the outgoing halfedges of the vertex
do {
HalfedgeIter h_twin = h->twin(); // get the vertex of the current halfedge
test if connected
h = h_twin->next(); // move to the next outgoing halfedge of the vertex.
set halfedge vertex here
} while(h != v->halfedge()); // keep going until we're back at the beginning
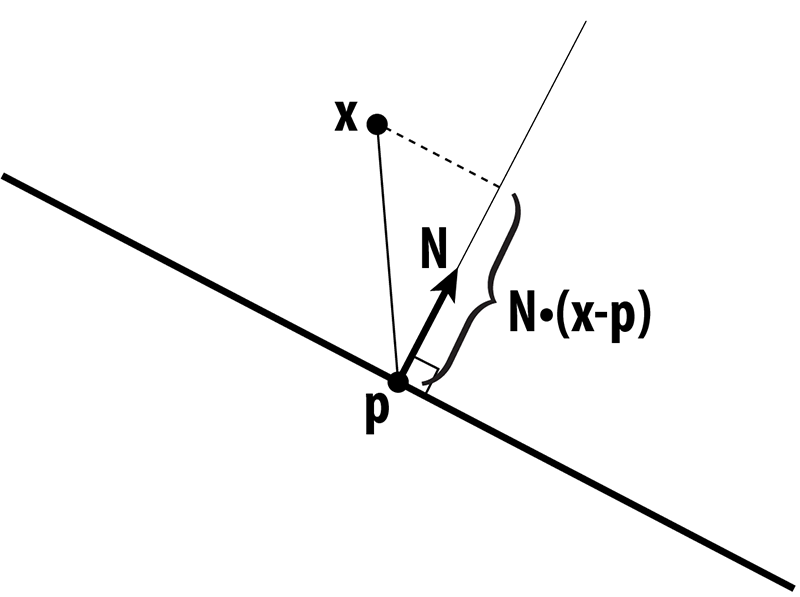
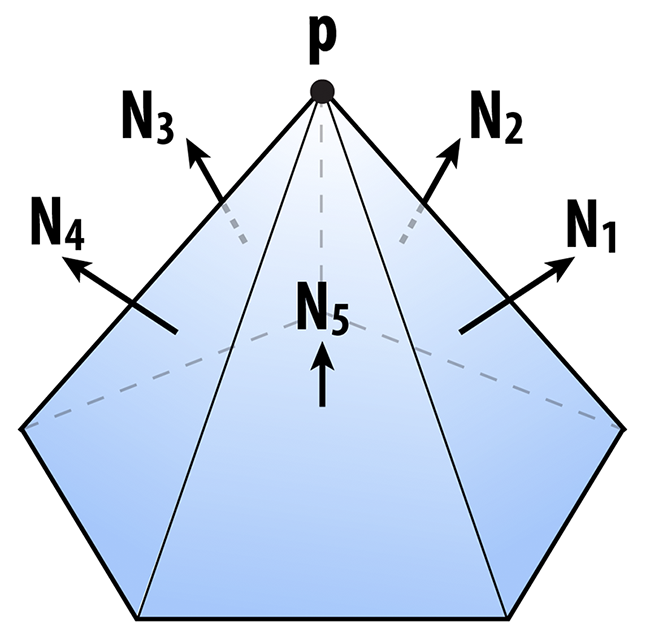
Quadric Error: Now that we can collapse edges the question is which edges to collapse. We want to collapse the edge that will change the mesh the least. To find this edge we must develop some measure of change. Quadric error is one measure of cost and the algorithm for using this measure to simplify meashes was developed by Michael Garland and Paul Heckbert. This is the algorithm that we use in Meshedit++. The main idea for quadric error is calculating the distance from any point to a plane, and summing these distances for each vertex. For a plane point x, normal N, and point p, the equation for calculating the distance from p to the plane is given by:
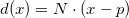
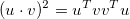
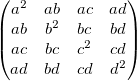
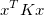
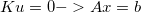
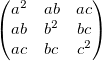
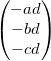
while(mesh.nFaces() > set_faces) {
// Get the cheapest edge from the queue.
bestEdge = queue.top();
// Remove the cheapest edge from the queue by calling pop().
queue.pop();
// Compute the new quadric by summing the quadrics at its two endpoints.
K = v1_quadric+v2_quadric
// Remove any edge touching either of its endpoints from the queue.
for v1 and v2 {
//Remove touching edges.
queue.remove(edge);
}
// Collapse the edge and set position to optimal point.
v = collapseEdge(bestEdge)
v_position = bestEdge_optimalPoint
// Set the quadric of the new vertex to the quadric computed in Step 2.
v_quadric = K;
// Insert any edge touching the new vertex into the queue, creating new edge records for each of them.
for (any edges touching v) {
queue.insert(edge);
}
}
- Visualizing the point cloud is not necessary for debugging mesh reconstruction, and hence should be a lower priority.
- When implementing extra classes for processing PolygonSoup objects, be sure unit test each objects of each type of class.
- When dealing with Halfedge structures make sure to account for all of your pieces or you can run into infinite loops and seg faults.
- There are cases where an edge collapse can cause a mesh to be non-manifold and some of these cases are hard to implement checks for.
| Command | Key |
| Display point cloud | P |
| Build Mesh | B |
| Collapse | C |
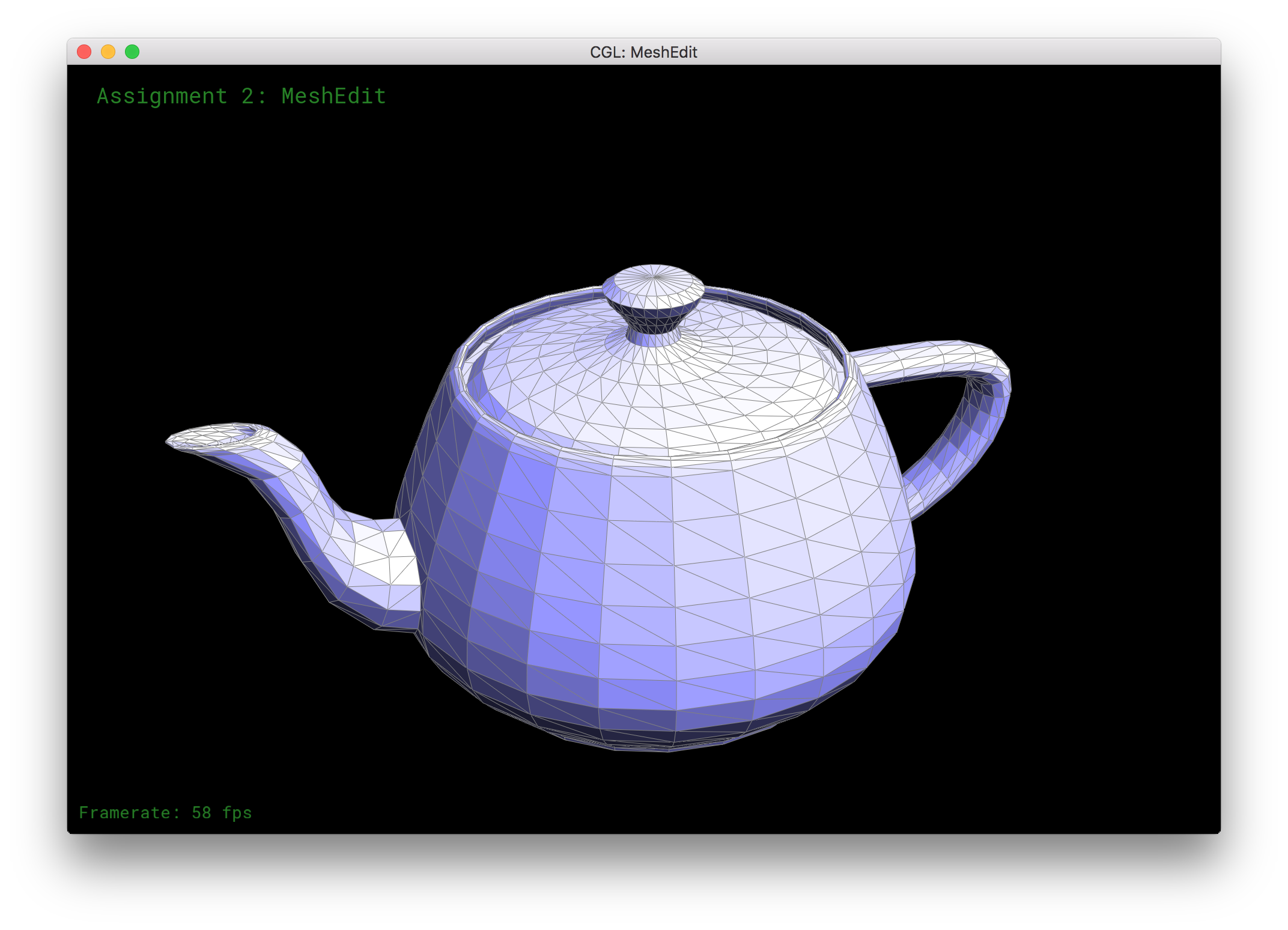
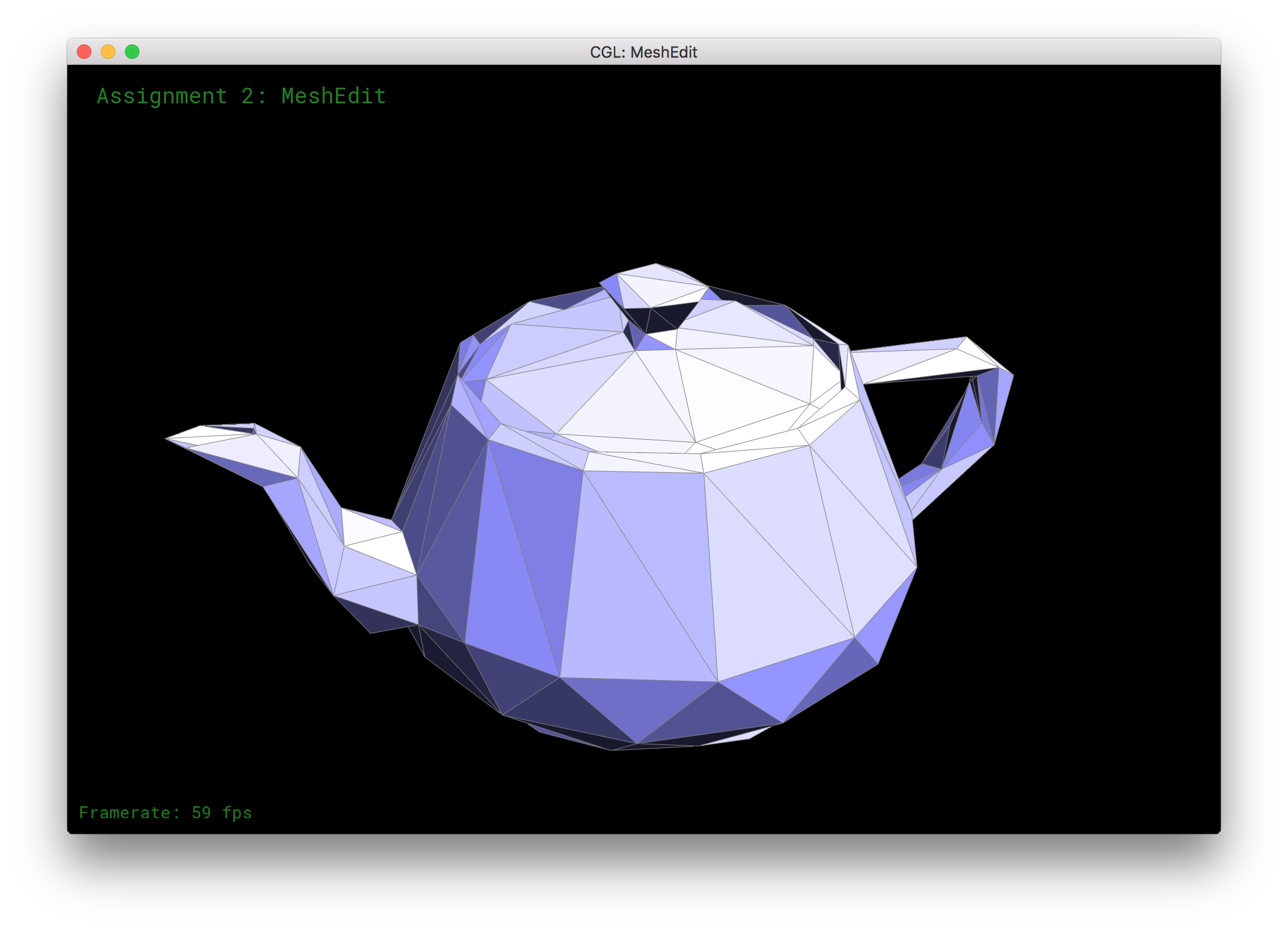
| Simplify Mesh | - |
- Jasper: Hacked the meshedit files to have the editor render point clouds. Helped write and debug mesh reconstruction.
- Annalise: Implemented all of the mesh simplification step of the pipeline.
- Matthew: Helped write and debug mesh reconstruction. Implemented the geometry-heavy parts of mesh reconstruction, such as point finding during ball pivoting.